正負の数の足し算、
(+3)+(+4)とか、(-3)+(-5)とか、
教科書通りやると、「同符号の足し算はね、絶対値の和に同じ符号を付けるんだよ」
(-3)+(+4)とか、(+3)+(-7)とか、
教科書通りやると、「異符号の足し算はね、絶対値の差に絶対値が大きい方の符号を付けるんだよ」
と、なんか、決まっているんだよ、覚えてね、と教えていたらつまらない。生徒を伸ばせない。
先程、補習をした体験生は、すごくセンスあった。
まず、負の数の導入
5-3=
できるよね?小学校の算数だもんね。
じゃ、3-5=
これはどうなる?
一瞬考えるけど、大体の子は感覚で知っている。-2?と答えてくれた。
そうそう。
中学になって「数学」になると、数が広がるんだ。
もちろん、見たこと聞いたことあると思うけど、負の数、マイナスが付くんだね。
ってか、なんで3-5=-2って思ったの?
「え、、数直線みたいなので考えてみました」
おお、、、教科書通り!
じゃ、990-1230= これは数直線でやっていたら大変だよね。どうやって計算する?
「1230から990をひきます、そして、マイナスをつければいいのかな・・・」
そのとおり!
じゃ、これは?
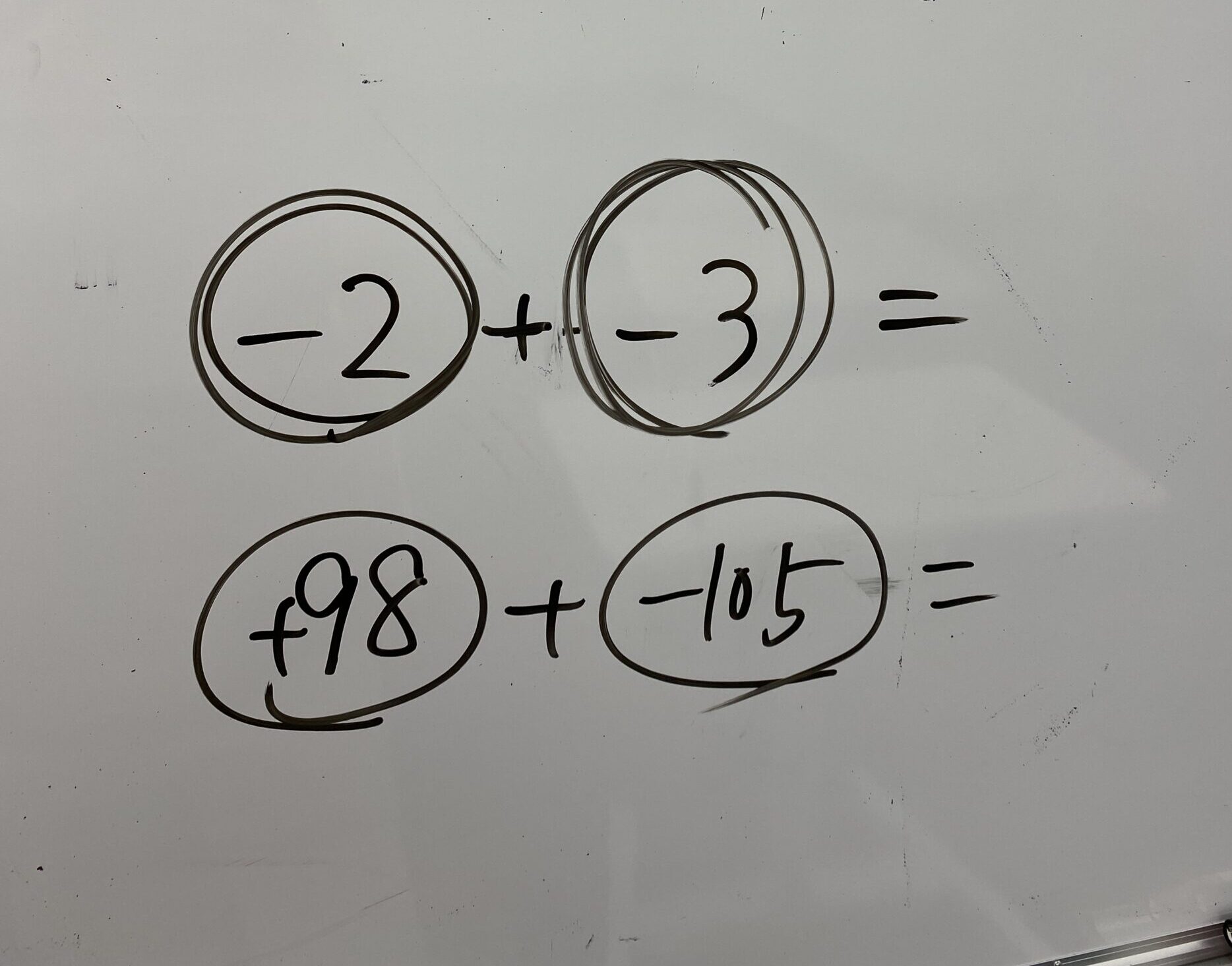
この足し算引き算も考えてみよう。
「え~、上は-5かな。。。」
そのとおり!頭の中を説明して!
「2と3を足しました。そして、マイナスがあるので、つけました」
すばらしい!今の導き方完璧!
下は?
「え~と、、、、105から98をひきました。それで、たぶんマイナスが付くのかな???」
その通り!
この子は、頭の中で感覚的にやったことを言葉に表す力もしっかりあります。
伸びますね。
で、結局
正負の数の足し算、
(+3)+(+4)とか、(-3)+(-5)とか、
教科書通りやると、「同符号の足し算はね、絶対値の和に同じ符号を付けるんだよ」
(-3)+(+4)とか、(+3)+(-7)とか、
教科書通りやると、「異符号の足し算はね、絶対値の差に絶対値が大きい方の符号を付けるんだよ」
ここの部分を自分で考え出したわけです。それをノートにまとめます。
こんな授業楽しいよね。決まりを言われてその通り計算しまくるより。
あ~、我ながら良い授業をした。笑
